Олимпиадная задача по стереометрии для 8–9 класса: сечение пирамиды плоскостью
Задача
В правильной треугольной пирамиде ABCD угол ADB равен2 arcsin 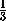 , а сторона основания ABC равна 2.
Точки K , M и N – середины отрезков AB , DK , AC соответственно. Точка E лежит на отрезке CM и3ME=CE .
Через точку E проходит плоскость Π перпендикулярно отрезку CM . В каком отношении плоскость Π делит рёбра пирамиды? Найдите площадь сечения пирамиды
плоскостью Π и расстояние от точки N до плоскости Π .
, а сторона основания ABC равна 2.
Точки K , M и N – середины отрезков AB , DK , AC соответственно. Точка E лежит на отрезке CM и3ME=CE .
Через точку E проходит плоскость Π перпендикулярно отрезку CM . В каком отношении плоскость Π делит рёбра пирамиды? Найдите площадь сечения пирамиды
плоскостью Π и расстояние от точки N до плоскости Π .
Решение
Решение задачи отсутствует
Ответ
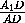 =
= 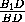 =
= 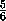 ,
, 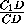 =
= 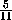 ,
, 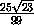 ,
, 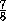 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет