Олимпиадная задача по стереометрии: разрез пирамиды через точку E, 8-9 класс
Задача
В правильной треугольной пирамиде ABCD угол ADC равен2 arcsin 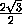 , а сторона основания ABC равна 2.
Точки K , M и N – середины рёбер AB , CD , AC соответственно. Точка E лежит на отрезке KM и3ME=KE .
Через точку E проходит плоскость Π перпендикулярно отрезку KM . В каком отношении плоскость Π делит рёбра пирамиды? Найдите площадь сечения пирамиды
плоскостью Π и расстояние от точки N до плоскости Π .
, а сторона основания ABC равна 2.
Точки K , M и N – середины рёбер AB , CD , AC соответственно. Точка E лежит на отрезке KM и3ME=KE .
Через точку E проходит плоскость Π перпендикулярно отрезку KM . В каком отношении плоскость Π делит рёбра пирамиды? Найдите площадь сечения пирамиды
плоскостью Π и расстояние от точки N до плоскости Π .
Решение
Обозначим 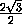 ADK = α ,
ADK = α , 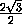 DCK = β ,
DCK = β , 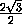 DKM = γ ,
DKM = γ , 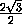 KMC = ϕ ,
KMC = ϕ , 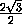 MKC = δ . Пусть DH – высота
пирамиды (рис.1). Тогда
MKC = δ . Пусть DH – высота
пирамиды (рис.1). Тогда
CK = 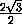 =
= 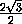 =
= 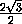 ,
CH =
,
CH = 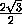 CK =
CK =  .
.
AD =  =
= 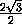 = 6,
DK =
= 6,
DK = 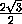 =
= 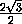 =
= 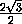 ,
,
cos β = 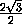 =
= 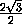 =
= 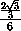 =
=
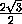 .
.
KM = 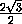 =
= 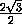 =
= 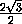 ,
,
cos γ = cos 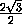 DKM =
DKM = 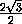 =
=
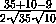 =
= 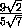 ,
,
EM = 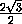 KM =
KM = 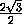 ,
KE =
,
KE = 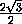 KM =
KM = 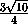 .
.
cos ϕ = cos 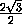 KMC =
KMC =  =
=
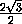 =
= 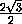 .
.
tg ϕ = 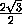 =
=  =
=
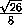 ,
,
tg γ =  =
= 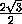 =
=
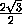 .
.
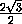 KM .
Из прямоугольного треугольника MEC1находим, что
KM .
Из прямоугольного треугольника MEC1находим, что
MC1 = 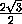 =
= 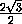 =
=
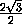 < 3 = MC.
< 3 = MC.
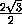 =
= 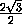 =
=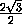 =
= 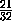 .
.
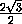 l , а т.к. прямая KC – ортогональная проекция наклонной KM на плоскость ABC , то по теореме о трёх перпендикулярах KC
l , а т.к. прямая KC – ортогональная проекция наклонной KM на плоскость ABC , то по теореме о трёх перпендикулярах KC 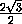 l , значит, l || AB и прямая l параллельна плоскости ABD . Следовательно, проходящая
через прямую l плоскость Π пересекается с плоскостью ABD по прямой, параллельной l , а значит, и прямой AB , т.е. A1B1 || AB .
l , значит, l || AB и прямая l параллельна плоскости ABD . Следовательно, проходящая
через прямую l плоскость Π пересекается с плоскостью ABD по прямой, параллельной l , а значит, и прямой AB , т.е. A1B1 || AB .
Из прямоугольного треугольника KEQ находим, что
KQ = 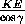 =
= 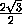 =
=
 .
.
 =
= 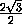 =
= 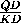 =
=
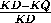 =
=  =
= .
.
EQ = KE tg γ = 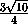 ·
· 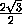 =
=
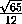 ,
,
EC1 = ME tg ϕ = 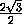 ·
· 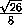 =
=
 .
.
C1Q = EQ+EC1 =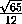 +
+ =
=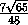 ,
,
A1B1 = 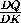 · AB =
· AB =  · 2 =
· 2 =  ,
,
SΔ A1B1C1=  A1B1· C1Q =
A1B1· C1Q =
 ·
·  ·
· 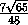 =
=
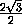 .
.
cos δ = cos 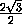 MKC =
MKC = 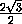 =
=
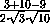 =
= 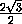 .
.
Опустим перпендикуляр TP из точки T на прямую KM . Из прямоугольного треугольника KPT находим, что
KP = KT cos δ =  ·
· 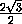 =
=  .
.
TL = PE = KE-KP = 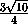 -
- =
= 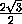 =
=
 .
.
Ответ
 =
= 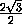 =
=  ,
, 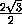 =
= 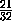 ,
, 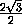 ,
,  .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь