Олимпиадная задача по стереометрии для 8-9 класса: правильная треугольная пирамида
Задача
В правильной треугольной пирамиде ABCD сторона
основания ABC равна 12, 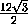 ADB = 2 arctg
ADB = 2 arctg 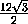 .
В треугольнике ABD проведена биссектриса BA1, а в
треугольнике BCD проведены медиана BC1и высота CB1. Найдите:
.
В треугольнике ABD проведена биссектриса BA1, а в
треугольнике BCD проведены медиана BC1и высота CB1. Найдите:
-
объём пирамиды A1B1C1D ;
-
площадь проекции треугольника A1B1C1на плоскость ABC .
Решение
Пусть M – середина AB (рис.1), H – центр равностороннего треугольника ABC . Обозначим 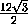 ADB = ϕ . Тогда
ADB = ϕ . Тогда
AH = 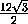 CM =
CM = 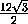 ·
·  = 4
= 4 ,
,
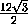 ADM =
ADM = 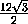 ,
tg
,
tg 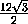 =
= 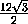 ,
,
cos 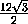 =
= 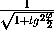 =
=
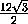 =
= 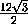 ,
sin
,
sin 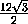 =
= 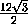 ,
cos ϕ =
,
cos ϕ = 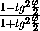 =
=
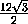 =
= 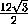 .
.
AD = 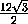 =
=  = 10,
DH =
= 10,
DH = 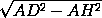 =
= 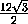 = 2
= 2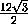 .
.
VABCD = 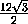 SΔ ABC· DH =
SΔ ABC· DH =
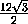 ·
· 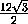 · 2
· 2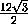 = 24
= 24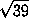 .
.
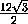 =
= 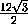 =
=
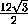 =
= 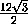 , поэтому
, поэтому 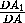 =
= 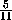 .
Из прямоугольного треугольника CB1D находим, что
.
Из прямоугольного треугольника CB1D находим, что 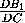 = cos ϕ =
= cos ϕ =
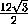 , поэтому
, поэтому 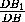 =
= 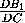 =
= 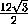 , а т.к.
, а т.к. 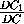 =
= 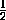 ,
то
,
то
VA1B1C1D = 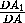 ·
· 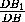 ·
· 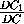 VABCD=
VABCD=
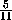 ·
· 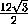 ·
· 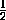 · 24
· 24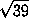 =
=  .
.
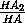 =
= 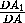 =
= 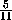 ,
,
 =
= 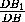 =
= 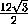 ,
,
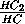 =
= 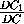 =
= 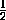 .
.
SΔ A2HB2= 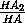 ·
·  SΔ AHB =
SΔ AHB =
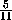 ·
· 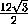 ·
· 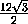 SΔ ABC,
SΔ ABC,
SΔ B2HC2=  ·
· 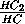 SΔ BHC =
SΔ BHC =
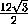 ·
· 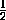 ·
· 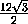 SΔ ABC,
SΔ ABC,
SΔ A2HC2= 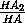 ·
· 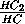 SΔ AHC =
SΔ AHC =
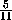 ·
· 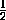 ·
· 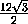 SΔ ABC.
SΔ ABC.
SΔ A2B2C2 = SΔ A2HB2+SΔ B2HC2+
SΔ A2HC2 =
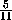 ·
· 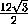 ·
· 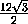 SΔ ABC+
SΔ ABC+
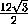 ·
· 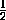 ·
· 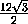 SΔ ABC+
SΔ ABC+
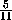 ·
· 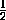 ·
· 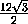 SΔ ABC=
SΔ ABC=
=(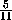 ·
· 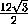 +
+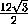 ·
· 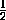 +
+
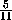 ·
· 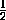 )·
)· 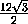 · SΔ ABC=
(
· SΔ ABC=
(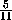 ·
· 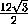 +
+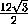 ·
· 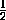 +
+
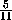 ·
· 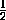 )·
)· 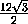 ·
· 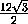 =
=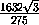 .
.
Ответ
 ,
, 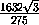 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь