Олимпиадная задача по стереометрии: радиус описанной сферы около пирамиды SABC
Задача
В шаре радиуса 9 через точку S проведены три равные хорды AA1, BB1и CC1так, что AS = 4, A1S = 8, BS < B1S , CS < C1S . Найдите радиус сферы, описанной около пирамиды SABC .
Решение
Произведения отрезков пересекающихся хорд равны, поэтому BS· SB1 = AS· SA1= 4· 8 = 32. Кроме того, BB1=AA1= AS+SA1 = 4+8 = 12. Из системы
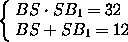
Пусть A2, B2и C2– основания перпендикуляров, опущенных из центра O сферы на хорды AA1, BB1и CC1соответственно. Тогда точки A2, B2и C2– середины этих хорд.
Заметим, что треугольная пирамида SABC подобна треугольной пирамиде SA2B2C2, т.к. эти пирамиды гомотетичны с центром гомотетии S и коэффициентом
k=-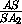 = -
= - = -
= - = -2.
= -2.
Отрезок OS виден из точек A2, B2и C2под прямым углом, значит, эти точки лежат на сфере с диаметром OS , т.е. OS – диаметр сферы, описанной около пирамиды SA2B2C2. Из прямоугольных треугольников AOA2и OSA2находим, что
OA22 = OA2-AA22 = OA2-( AA1)2 =
92-62 = 45,
AA1)2 =
92-62 = 45,
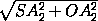 =
=  = 7.
= 7.
Ответ
7.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь