Олимпиадная задача по стереометрии: максимальный объём пирамиды с квадратным основанием
Задача
Основание пирамиды – квадрат. Высота пирамиды пересекает диагональ основания. Найдите наибольший объём такой пирамиды, если периметр диагонального сечения, содержащего высоту пирамиды, равен 5.
Решение
Лемма: Из всех треугольников с заданными основанием и периметром
наибольшую площадь (а значит, и высоту) имеет равнобедренный.
Доказательство леммы: Пусть x , y и z – стороны треугольника,
z – его заданная сторона, S – высота, p=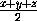 –
заданный полупериметр треугольника. По формуле Герона
–
заданный полупериметр треугольника. По формуле Герона
S = 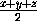 =
= 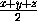 ·
· 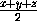 =
k
=
k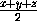 ,
,
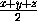 – фиксированная величина. Тогда
– фиксированная величина. Тогда
S =k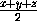
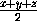 k·
k· 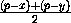 =
k·
=
k· 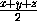 = kz,
= kz,
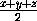 .
.
Пусть V(a) – этот объём. Тогда
V(a) = 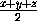 AB2· PH =
AB2· PH =
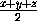 a2·
a2· 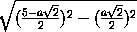 =
=
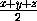 a2
a2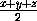 .
.
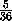 a4(5-2a
a4(5-2a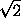 )на луче(0; +
)на луче(0; +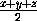 ):
):
f'(a) = 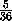 (4a3(5-2a
(4a3(5-2a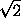 ) - 2a4
) - 2a4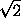 ) =
) =
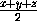 a3(
a3(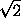 -a).
-a).
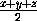 )принадлежит единственная критическая точка a=
)принадлежит единственная критическая точка a=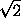 этой
функции, причём при переходе через эту точку производная меняет знак с "+" на "-".
Следовательно, a=
этой
функции, причём при переходе через эту точку производная меняет знак с "+" на "-".
Следовательно, a=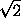 – точка максимума. Тогда и функция V(a)принимает
в этой точке наибольшее значение, которое равно
– точка максимума. Тогда и функция V(a)принимает
в этой точке наибольшее значение, которое равно
V(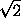 )=
)= 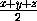 · 2
· 2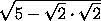 =
= 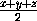 .
.
Ответ
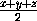 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет