Олимпиадная задача по стереометрии: радиусы шаров через стороны треугольника
Задача
Три шара касаются некоторой плоскости и попарно касаются друг друга. Найдите радиусы шаров, если известно, что точки касания шаров с плоскостью являются вершинами треугольника со сторонами a , b и c .
Решение
Решение задачи отсутствует
Ответ
Пусть O1, O2и O3– центры данных шаров, x , y и z соответственно – их радиусы, A , B и C соответственно – точки касания шаров с общей касательной плоскостью, AB=c , AC=b , BC=a .
Отрезки O1A и O1B – радиусы, проведённые в точки касания с касательной плоскостью, поэтому O1A || O1B . Рассмотрим сечение шаров с центрами O1и O2плоскостью, проходящей через параллельные прямые O1A и O1B . Получим касающиеся внешним образом окружности с центрами O1и O2и прямую, касающуюся этих окружностей в точках A и B . Тогда
с = AB = 2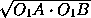 = 2
= 2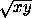 .
.
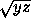 и b = 2
и b = 2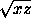 . Из системы
. Из системы

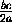 , y=
, y=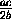 , z=
, z= .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь