Олимпиадная задача по стереометрии для 10-11 класса: пропорции объёмов пирамид
Задача
На боковых рёбрах SA , SB и SC четырёхугольной пирамиды SABCD , основание которой есть квадрат, взяты соответственно точки A1, B1и C1так, что SA1:SA=3:7, SB1:SB = 2:7и SC1:SC = 4:9. Плоскость, проходящая через точки A1, B1и C1пересекает ребро SD в точке D1. Найдите отношение SD1:SD и отношение объёма пирамиды SA1B1C1D1к объёму пирамиды SABCD .
Решение
Обозначим VSABCD = V ,  = x . Плоскость диагонального
сечения SAC пирамиды разбивает её на две равновеликие пирамиды, поэтому VSABC = VSACD =
= x . Плоскость диагонального
сечения SAC пирамиды разбивает её на две равновеликие пирамиды, поэтому VSABC = VSACD = 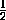 V . Тогда
V . Тогда
VSA1B1C1 =
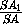 ·
· 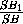 ·
· 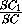 · VSABC
=
· VSABC
= 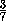 ·
· 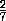 ·
· 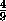 ·
· 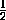 V=
V=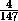 V,
V,
VSA1D1C1 =
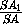 ·
· 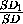 ·
· 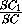 · VSADC
=
· VSADC
= 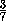 · x ·
· x · 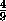 ·
· 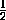 V=
V=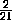 Vx.
Vx.
VSA1B1D1 =
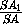 ·
· 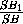 ·
· 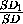 · VSABD
=
· VSABD
= 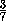 ·
· 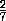 · x·
· x· 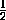 V=
V=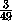 Vx,
Vx,
VSB1D1C1 =
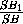 ·
· 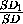 ·
· 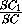 · VSBDC
=
· VSBDC
= 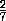 · x ·
· x · 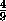 ·
· 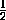 V=
V=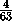 Vx,
Vx,
VA1B1C1D1 =VSA1B1C1+VSA1D1C1 = VSA1B1D1+VSB1D1C1,
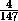 V+
V+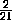 Vx =
Vx = 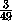 Vx+
Vx+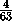 Vx,
Vx,
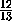 .
Тогда
.
Тогда
VSA1B1C1D1 = VSA1B1C1+VSA1D1C1=
=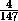 V+
V+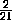 Vx =
Vx = 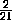 (
(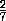 +
+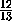 )V=
)V=
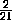 ·
· 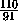 V =
V = 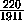 V.
V.
Ответ
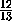 ;
; 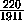 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь