Олимпиадная задача по стереометрии для 10-11 классов: объем пирамиды EKLF
Задача
Выпуклый многогранник ABCDFE имеет пять граней: CDF , ABE , BCFE , ADFE и ABCD . Ребро AB параллельно ребру CD . Точки K и L расположены соответственно на рёбрах AD и BC так, что отрезок KL делит площадь грани ABCD пополам. Точка M является серединой ребра EF и вершиной пирамиды MABCD , объём которой равен 6. Найдите объём пирамиды EKLF , если известно, что объём многогранника ABCDFE равен 19.
Решение
Пусть E1, M1и F1– ортогональные проекции точек
соответственно E , M и F на плоскость параллельных прямых AB и CD . Тогда EE1– высота четырёхугольной пирамиды EAKLB с вершиной E , MM1– высота четырёхугольной пирамиды MABCD с вершиной M , FF1– высота четырёхугольной пирамиды FCDKL с вершиной F .
Обозначим EE1=a , MM1=b , FF1=c , SABCD = S . Из условия
задачи следует, что VABCD = 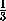 S· b = 6.
S· b = 6.
Поскольку M – середина отрезка EF , M1– середина отрезка E1F1. Поэтому
b = MM1 = 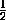 (EE1+FF1) =
(EE1+FF1) = 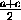 .
.
VEKLF = VABCDFE - VEAKLB-VFCDKL =
19-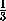 SABLK· a -
SABLK· a -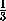 SCDKL· c=
SCDKL· c=
=19-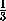 (
(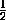 S· a +
S· a + 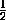 S· c)=
19-
S· c)=
19-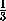 S·
S· 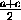 = 19-
= 19-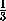 S· b =
S· b =
=19-VMABCD = 19-6 = 13.
Ответ
13.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь