Олимпиадная задача по стереометрии: пересечение плоскостей призмы и расстояния
Задача
Дано изображение призмы ABCA1B1C1. Постройте изображение точки M пересечения плоскостей A1BC , AB1C и ABC1. Пусть высота призмы равна h . Найдите расстояние от точки M до оснований призмы.
Решение
Будем считать, что точки A , B , C , A1, B1, C1, M и есть изображения вершин призмы. Пусть P и Q – центры граней AA1B1B и AA1C1C . Точки C и P – общие точки плоскостей A1BC и AB1C , поэтому плоскости A1BC и AB1C пересекаются по прямой CP . Точки B и Q – общие точки плоскостей A1BC и ABC1, поэтому плоскости A1BC и ABC1пересекаются по прямой BQ . Прямые CP и BQ лежат в плоскости A1BC . Точка M их пересечения есть точка пересечения плоскостей A1BC , AB1C и ABC1. Так как P – середина A1B , а Q – середина A1C , то CP и BQ – медианы треугольника A1BC . Значит, M – точка пересечения медиан треугольника A1BC .
Пусть D и D1– ортогональные проекции точки M на параллельные плоскости соответственно ABC и A1B1C1. Тогда DD1– высота призмы. Медиана A1R треугольника A1BC делится точкой M в отношении 2:1. Отрезки A1R и D1D с концами в параллельных плокостях A1B1C1и ABC пересекаются в точке M . Значит, D1M:DM = 2:1. Следовательно,
DM = 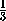 DD1 =
DD1 = 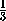 h,
D1M =
h,
D1M = 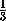 DD1 =
DD1 = 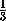 h.
h.
Ответ
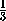 h ;
h ; 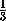 h .
h .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь