Олимпиадная задача: Точка пересечения диагоналей четырёхугольника ABCD (планиметрия, 8-9 класс)
Задача
На плоскости даны точки A(1;2), B(2;1), C(3;-3), D(0;0). Они являются вершинами выпуклого четырёхугольника ABCD . В каком отношении точка пересечения его диагоналей делит диагональ AC ?
Решение
Поскольку прямые AC и BD не параллельны оси OY , их уравнения можно найти в виде y=ax+b . Подставив координаты точек A и C в это уравнение, получим систему
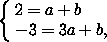
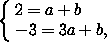 , b=
, b=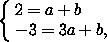 .
.
Аналогично получим уравнение прямой BC : y=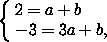 x .
x .
Координаты точки M пересечения прямых AC и BD находим из системы
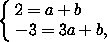
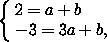

 и
и 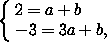 . Поскольку
координаты вектора равны разностям соответствующих координат конца
и начала, то
. Поскольку
координаты вектора равны разностям соответствующих координат конца
и начала, то
 = (
= (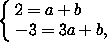 - 1;
- 1; 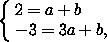 -2)=
(
-2)=
(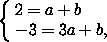 ; -
; -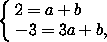 ),
),
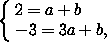 = (3 -
= (3 - 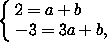 ; -3-
; -3-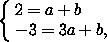 )=
(
)=
(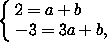 ; -
; -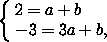 ).
).
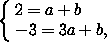 =3
=3 .
Значит, точка M делит диагональ AC в отношении3:1, считая от точки A .
.
Значит, точка M делит диагональ AC в отношении3:1, считая от точки A .
Ответ
1:3, считая от точки A .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет