Назад

Олимпиадная задача по планиметрии: максимальная площадь фигуры в задаче с дугой BC

Задача 210924 • Сложность: 3 • 9-11 класс
Задача

На рисунке изображена фигура ABCD . Стороны AB , CD и AD этой фигуры– отрезки (причём AB||CD и AD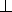 CD ); BC – дуга окружности, причём любая касательная к этой дуге отсекает от фигуры трапецию или прямоугольник. Объясните, как провести касательную к дуге BC , чтобы отсекаемая фигура имела наибольшую площадь.

Разделы:
Планиметрия
Источники:
Турнир им.Ломоносова Олимпиады и турниры 30 (2007), математика
Количество версий:
4
Решение

Воспользуемся формулой площади трапцеии – площадь равна произведению средней линии на высоту.

В нашем случае боковыми сторонами трапеции будут отрезок AD и касательная MN , а основаниями трапеции – отрезки (Эти отрезки на чертеже расположены вертикально, а не горизонтально, что стилистически менее привычно для названия "основание трапеции". Тем не менее ничто не мешает формально рассмотреть отрезки AM и DN качестве оснований трапеции.) AM и DN .

Очевидно, что высота трапеции (расстояние между основаниями, равное, например, перпендикулярному основаниям отрезку AD ) не зависит от выбора положения касательной. А вот среднюю линию можно менять.

Проведём серединный перпендикуляр к AD . Обозначим точки его пересечения с AD и c дугой BC через K и L соответственно. Заметим, что средняя линия получаемых трапеций всегда будет содержаться в отрезке KL .

Значит, площадь максимальна, если средняя линия совпадет с KL . Поэтому следует провести касательную через точкуL.
Ответ

Касательную к дуге BC надо провести через точку пересечения этой дуги с серединным перпендикуляром к отрезку AD .

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет