Олимпиадная задача: перенумерация точек на плоскости и углы между векторами
Задача
На плоскости даны точки A1 , A2 , An и точки B1 , B2 , Bn . Докажите, что точки Bi можно
перенумеровать так, что для всех i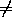 j угол между векторами
j угол между векторами 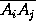 и
и 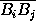 – острый или прямой.
– острый или прямой.
Решение
Выберем на плоскости начало координат O и рассмотрим сумму S=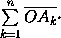
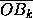 .
Выберем такую нумерацию точек Bi , что соответствующая сумма S максимальна. Рассмотрим теперь нумерацию точек B , в которой Bi и Bj обозначены Bj и Bi и ее сумму S' . По предположению максимальности S
.
Выберем такую нумерацию точек Bi , что соответствующая сумма S максимальна. Рассмотрим теперь нумерацию точек B , в которой Bi и Bj обозначены Bj и Bi и ее сумму S' . По предположению максимальности S S' , но
S' , но
S-S'=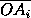 ·
· 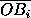 +
+
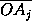 ·
· 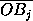 -
-
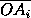 ·
· 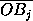 -
-
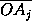 ·
· 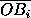
 0.
0.
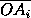 -
-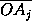 )·
(
)·
(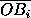 -
-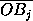 )=
AjAi·
)=
AjAi· 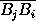
 0.
(*)
0.
(*)Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет