Олимпиадная задача по стереометрии: площадь основания пирамиды наименьшего объёма
Задача
Плоскость проходит через сторону основания правильной четырёхугольной пирамиды и делит пополам двугранный угол при этой стороне. Найдите площадь основания пирамиды наименьшего объёма, если известно, что указанная плоскость пересекает высоту пирамиды в точке, удалённой на расстояние d от плоскости основания.
Решение
Пусть плоскость, проходящая через сторону AB основания ABCD правильной четырёхугольной пирамиды PABCD пересекает высоту PM пирамиды в точке K , причём MK = d . Рассмотрим сечение пирамиды плоскостью, проходящей через апофемы PG и PH лежащие в гранях APB и CPD . Тогда PGH – линейный угол двугранного угла между плоскостью боковой грани пирамиды и плоскостью основания, а GK – биссектриса этого угла.
Обозначим  KGM = α , PM=h , AB=a . Тогда
KGM = α , PM=h , AB=a . Тогда
 PGM = 2α, MG =
PGM = 2α, MG = 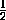 GH =
GH = 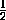 AB =
AB = 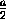 .
.
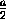 =MG =
=MG = 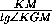 =
= 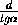 ,
,
h=PM = MG tg  PGM =
PGM = 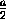 · tg 2α =
· tg 2α =
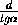 ·
· 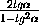 =
=
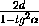 .
.
VPABCD = 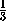 SABCD· h =
SABCD· h =
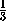 a2h =
a2h = 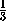 ·
· 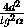 ·
· 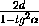 =
=
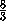 d3 ·
d3 · 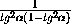 .
.

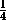 ,
причём равенство достигается при t=
,
причём равенство достигается при t=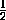 , то
, то
VPABCD = 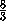 d3 ·
d3 · 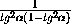 =
=
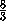 d3 ·
d3 · 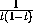

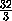 d3,
d3,
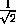 Тогда
Тогда
SABCD = a2 = 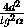 = 4d2· 2 = 8d2.
= 4d2· 2 = 8d2.
Ответ
8d2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь