Олимпиадная задача по стереометрии: расстояние от точки до плоскости в кубе для 10-11 классов
Задача
Ребро куба EFGHE1F1G1H1равно 2. На рёбрах EH и HH1взяты точки A и B , причём 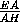 =2,
=2, 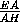 =
= 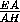 . Через точки A , B и G1проведена плоскость. Найдите расстояние от точки E до этой
плоскости.
. Через точки A , B и G1проведена плоскость. Найдите расстояние от точки E до этой
плоскости.
Решение
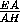 Поскольку
Поскольку 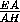 =
= 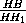 , прямая AB параллельна
диагонали H1E квадрата EHH1E1, а т.к. H1E || G1F ,
то AB || G1F . Значит, прямые AB и G1F лежат в одной
плоскости – в секущей плоскости, проходящей через точки A , B и G1.
Таким образом, трапеция ABG1F – сечение, о котором говорится в условии
задачи.
, прямая AB параллельна
диагонали H1E квадрата EHH1E1, а т.к. H1E || G1F ,
то AB || G1F . Значит, прямые AB и G1F лежат в одной
плоскости – в секущей плоскости, проходящей через точки A , B и G1.
Таким образом, трапеция ABG1F – сечение, о котором говорится в условии
задачи.
Пусть K – точка пересечения AF и EG . Тогда секущая плоскость и плоскость диагонального сечения EGG1E1пересекаются по прямой G1K . Прямая G1K пересекает лежащую с ней в плоскости EGG1E1прямую EE1в некоторой точке D . Тогда искомое расстояние от точки E до плоскости ABG1F равно высоте тетраэдра DAFE , проведённой из вершины E .
Из подобия треугольников AKE и FKG следует, что
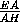 =
= 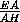 =
= 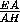 =
= 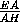 .
.
DE = GG1· 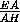 =GG1·
=GG1· 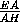 =
=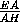 · 2=
· 2=
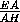 .
.
DF=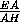 =
= 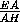 =
= 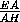 ,
,
AF=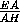 =
= 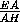 =
= 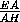 ,
,
AD = AE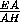 =
= 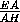 .
.
FP = 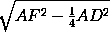 =
= 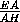 =
= 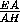 =
=
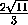 .
.
V=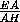 SΔ DEF· AE =
SΔ DEF· AE = 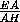 ·
· 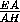 DE· EF · AE=
DE· EF · AE=
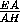 ·
· 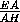 · 2·
· 2· 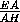 =
= 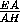 .
.
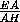 SΔ ADF· h , где h – искомое расстояние.
Следовательно,
SΔ ADF· h , где h – искомое расстояние.
Следовательно,
h = 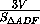 =
= 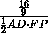 =
=
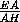 =
2
=
2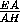 .
.
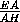 Введём систему координат Oxyz , направив ось Ox по лучу HG , ось Oy –
по лучу HE , ось Oz – по лучу HH1. Найдём координаты нужных нам точек: G1(2;0;2), E(0;2;0). Запишем уравнение плоскости ABG1в отрезках:
Введём систему координат Oxyz , направив ось Ox по лучу HG , ось Oy –
по лучу HE , ось Oz – по лучу HH1. Найдём координаты нужных нам точек: G1(2;0;2), E(0;2;0). Запишем уравнение плоскости ABG1в отрезках:
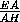 +
+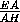 +
+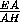 =1.
=1.
-x+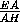 y+
y+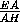 z= 1, или2x-3y-3z+2=0.
z= 1, или2x-3y-3z+2=0.
h=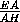 =
=
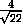 =2
=2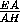 .
.
Ответ
2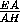 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь