Назад

Олимпиадная задача по планиметрии: углы треугольника A₁B₁C₁, медианы, 7–9 класс

Задача 210225 • Сложность: 3 • 7-9 класс
Задача

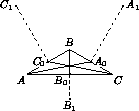
Медиану AA0 треугольника ABC отложили от точки A0 перпендикулярно стороне BC во внешнюю сторону треугольника. Обозначим второй конец построенного отрезка через A1. Аналогично строятся точки B1 и C1. Найдите углы треугольника A1B1C1, если углы треугольника ABC равны 30°, 30° и 120°.

Авторы:
Емельянов Л. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2005-2006 Региональный этап
Количество версий:
5
Решение
Так как треугольникABCравнобедренный, тоBB0– серединный перпендикуляр к основаниюAC. Значит,B1лежит на этом перпендикуляре и  CB0⊥BB1.  Таким образом,CB0– высота и медиана треугольникаBCB1, откудаBC = B1C,  а так как  ∠B1BC= ½ ∠B= 60°,  то треугольникB1BC– равносторонний. A0, будучи серединой стороныBCявляется основанием высоты этого треугольника. Следовательно, точкиA1иB1лежат на серединном перпендикуляре к отрезкуBC. Аналогично,C1иB1лежат на серединном перпендикуляре к отрезкуAB. Значит,  ∠C1B1A1= 180° –B= 60°, B1A1=B1A0+A0A1=B1A0+A0A = B1C0+C0C = B1C0+C0C1=B1C1,  то есть треугольникA1B1C1– равнобедренный с углом при вершине 60°.
Ответ

Все углы равны 60°.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет