Олимпиадная задача по математике: правильные клетки и числа на клетчатой плоскости

  Предположим, что при некоторой расстановке чисел все клетки оказались правильными.

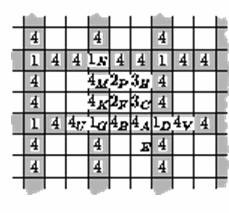
  Пусть в клетку A записано число 4, тогда в одной из соседних с A клеток, например, в клетку B, записано число 4, а в одну из клеток C, D, E – число 1. Если 1 записана в клетке C, то в клетку F также записано 4, что невозможно: у клетки B две соседних клетки с числом 4. Аналогично число 1 не может быть записано в клетку E. Значит, 1 – в клетке D. Аналогично 1 – в клетке G, а тогда в клетках U и V – опять четверки. Итак, числа 4 порождают цепочки  ...-1-4-4-1-4-4-... .

  Из того, что в клетку K записано число 4, следует, что в M записано 4, в N записано 1, и тогда однозначно восстанавливаются числа в выделенных строках и столбцах (см. рис.).

  В один из незаполненных еще квадратов 2×2 записано число 3. Пусть, для определенности, 3 записано в клеткуC. В клеткиFиHнельзя записать 1 и 4, значит, там записаны 2 и 3.   Без ограничения общности, пусть 2 записано вF, а 3 – вH.   Рассматривая клеткуH, получаем, что в клеткуPзаписано число 2. Но в этом случае у клеткиFс числом 2 в соседних клетках три различных числа. Противоречие.

Не могут.