Олимпиадная задача по планиметрии для 8-10 классов от Емельянова Л. А.

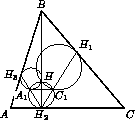
  Обозначим через H ортоцентр треугольника ABC, через H₁, H₂, H₃ – основания высот на сторонах BC, CA, AB соответственно, а через A₁, B₁, C₁ – вторые точки пересечения окружностей.

  Так как прямаяBC– касательная к окружности, проходящей черезHиH₁и  HH₁⊥BC,  тоHH₁– диаметр одной из окружностей, данных в условии. Аналогично для двух других окружностей.   Поэтому  ∠HC₁H₂+ ∠HC₁H₁= 90° + 90° = 180°,  то естьC₁лежит на отрезкеH₁H₂. Аналогично  A₁∈H₂H₃.  ТочкиB, H₂,H₃,Cлежат на окружности с диаметромBC, следовательно,  ∠HH₂A₁= ∠BH₂H₃= ∠BCH₃= 90° – ∠B.  Аналогично  ∠HH₂C₁= 90° – ∠B.   Значит, прямоугольные треугольникиHH₂A₁иHH₂C₁равны, а точкиA₁иC₁симметричны относительноHH₂.   Следовательно,  A₁C₁⊥HH₂,  откуда  A₁C₁||AC.  Аналогично  B₁C₁||BC  и  A₁B₁||AB,  что и доказывает подобие треугольников.

Ответ задачи отсутствует