Олимпиадная задача по алгебре: корни приведённых трёхчленов для 8–10 класса
Задача
Даны n > 1 приведённых квадратных трёхчленов x² – a1x + b1, ..., x² – anx + bn, причём все 2n чисел a1, ..., an, b1, ..., bn различны.
Может ли случиться, что каждое из чисел a1, ..., an, b1, ..., bn является корнем одного из этих трёхчленов?
Решение
Предположим, что это так. Поскольку все 2n коэффициентов различны, то они и составляют всё множество корней наших трёхчленов, причём у каждого из них два корня. Пусть xi, yi – корни трёхчлена x² – aix + bi. Тогда ai = xi + yi, bi = xiyi и
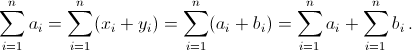Следовательно, 
Далее,
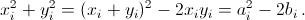Поэтому 
Значит,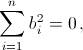 
то есть все коэффициенты bi равны нулю. Это противоречит тому, что они различны.
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет