Назад

Олимпиадная задача по стереометрии: перпендикуляры в тетраэдре и параллельность плоскостей

Задача 210204 • Сложность: 3 • 10-11 класс
Задача

В тетраэдре ABCD из вершины A опустили перпендикуляры AB' , AC' , AD' на плоскости, делящие двугранные углы при ребрах CD , BD , BC пополам. Докажите, что плоскость(B'C'D')параллельна плоскости(BCD).

Авторы:
Бадзян А. И.
Разделы:
Стереометрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2005-2006 Региональный этап
Количество версий:
5
Решение
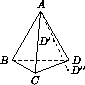
Продолжим отрезок AB' до пересечения с плоскостью BCD в точке B'' . Так как плоскости(BCD)и(ACD)симетричны относительно биссекторной плоскости, то AB'=B'B'' . Аналогично по точкам C' и D' строим точки C'' и D'' .

При гомотетии с центром A и коэффициентом 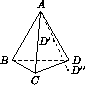плоскость(B''C''D'')переходит в плоскость(B'C'D'), поэтому(B'C'D')|| (B''C''D'')=(BCD), что и требовалось доказать.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет