Назад

Олимпиадная задача по планиметрии для 9–11 классов от Емельянова Л. А.

Задача 210199 • Сложность: 3 • 9-11 класс
Задача

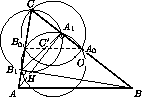
AA1 и BB1 – высоты остроугольного неравнобедренного треугольника ABC. Известно, что отрезок A1B1 пересекает среднюю линию, параллельную AB, в точке C'. Докажите, что отрезок CC' перпендикулярен прямой, проходящей через точку пересечения высот и центр описанной окружности треугольника ABC.

Авторы:
Емельянов Л. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2004-2005 Региональный этап
Количество версий:
4
Решение

  Пусть A0, B0 – середины сторон BC и CA, H – точка пересечения высот, O – центр описанной окружности.

  Как известно,  ∠CB1A1 = ∠B = ∠CA0B0,  следовательно, точки A1, B1, A0, B0 лежат на одной окружности Ω1. Кроме того, точки A1, B1 лежат на окружности Ω2 с диаметром CH, а точки A0, B0 – на окружности Ω3 с диаметром CO.

  ТочкаC'лежит на радикальных осях окружностей Ω1и Ω2, а также Ω1и Ω3, и, следовательно, является радикальным центром всех трёх окружностей. Центры окружностей Ω2и Ω3– серединыCHиCOсоответственно.   ПрямаяCC'как радикальная ось окружностей Ω2и Ω3перпендикулярна их линии центров, а значит, иHO .
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет