Олимпиадная задача по математике: отражение вершин трапеции и свойства трапеции
Задача
Каждую вершину трапеции отразили симметрично относительно диагонали, не содержащей эту вершину.
Докажите, что если получившиеся точки образуют четырёхугольник, то он также является трапецией.
Решение
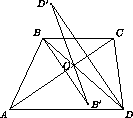
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет