Олимпиадная задача по планиметрии и делимости для 9–11 классов от Волченкова С. Г.

Решение 1:   Допустим, это возможно для прямоугольника ABCD. Пусть AB – его наименьшая сторона. Выберем начало координат в узле сетки и направим оси координат вдоль линий сетки так, чтобы среди вершин прямоугольника вершина A имела наименьшую абсциссу, а вершина B – наименьшую ординату. Через A_x, B_x, C_x, D_x и A_y, B_y, C_y, D_y обозначим проекции вершин на оси (см. рис.).

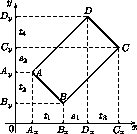
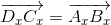  Абсциссы точекA_x, B_x, C_x, D_xи ординаты точекA_y, B_y, C_y, D_y– нецелые, так как вершиныA, B, C, Dне лежат на линиях сетки. Так как    и  A_xD_x = ADcos 45° ≥ABcos 45° =A_xB_x,  то точки на осиOxлежат в порядкеA_x, B_x, D_x, C_x. (B_xиD_xмогут совпасть.)   Точки на осиOyлежат в порядкеB_y, A_y, C_y, D_y. При этом  A_xB_x = D_xC_x = B_yA_y = C_yD_y = ABcos 45°, B_xD_x = A_yC_y= (AD – AB) cos 45°.   Черезt₁,t₂,t₃,t₄,s₁,s₂обозначим количество точек с целыми координатами соответственно на отрезкахA_xB_x, B_yA_y, D_xC_x, C_yD_y, B_xD_x, A_yC_y. На отрезкеA_xB_xровноt₁целочисленных точек, поэтому сторонаABпересекает ровноt₁вертикальных линий сетки; на отрезкеA_yD_y   t₄+s₂  целочисленных точек, следовательно, сторонаADпересекает ровно  t₄+s₂  горизонтальных линий сетки, и т.д. Таким образом, условие пересечения каждой стороной нечётного числа линий сетки эквивалентно нечётности чисел  t₁+t₂, t₃+t₄, t₁+t₄+s₁+s₂, t₂+t₃+s₁+s₂.   Лемма. Если два отрезка равной длины d расположены на числовой прямой так, что их концы нецелочисленны, то количества целых точек на этих отрезках отличаются не более чем на 1.

  Доказательство. Если на отрезке с левым концом в нецелой точке a и правым концом в нецелой точке b лежит k целых точек n,  n + 1,  ...,  n + k – 1,  то  n – 1 < a < n  и  n + k – 1 < b < n + k,  поэтому  k – 1 < d = b – a < k + 1  и  d – 1 < k < d + 1,  то есть  k = [d]  или  k = [d] + 1.   Из леммы следует, что числа t₁, t₂, t₃, t₄ отличаются не более чем на 1, то есть равны t или  t + 1,  и также числа s₁ и s₂ равны s или  s + 1.  Так как  t₁ + t₂  нечётно, то  t₁ ≠ t₂.  Пусть для определенности  t₁ = t,  t₂ = t + 1.

  Если  t₃ = t,  то  t₄ = t + 1,  так как  t₃ + t₄  нечётно. Тогда  s₁ + s₂ = (t₁ + t₄ + s₁ + s₂) – (t₁ + t₄) = (t₁ + t₄ + s₁ + s₂) – (2t + 1)  чётно. Отсюда  s₁ = s₂.  Но тогда  (t₂ + s₂ + t₄) – (t₁ + s₁ + t₃) = 2,  что противоречит лемме (для отрезков A_xC_x и B_yD_y).

  Если же  t₃ = t + 1,  то  t₄ = t.  Тогда  s₁ + s₂ = (t₁ + t₄ + s₁ + s₂) – (t₁ + t₄)  нечётно, то есть либо  s₁ = s,  s₂ = s + 1,  либо  s₁ = s + 1,  s₂ = s.  Оба случая противоречят лемме: первый – для отрезков A_xD_x и B_yC_y, второй – для отрезков B_xC_x и A_yD_y.

Решение 2:   Предположим, такой прямоугольник ABCD существует. Пусть 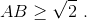    Отложим на сторонах AB и CD отрезки  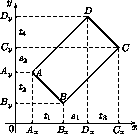  Тогда отрезки BB' и CC' пересекают по одной вертикальной и горизонтальной линии, а отрезок B'C' получается из BC переносом на вектор с целыми координатами. Поэтому прямоугольник AB'C'D также удовлетворяет условию.

  Продолжая такие действия, получим в результате прямоугольник, все стороны которого меньше 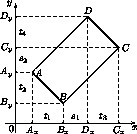   (обозначим его опять ABCD). Тогда каждая сторона пересекает не более одной прямой каждого направления, то есть ровно по одной прямой – либо вертикальной, либо горизонтальной.

  Пусть A – самая левая точка прямоугольника, а B – самая нижняя, тогда C – самая правая, а D – самая верхняя.

  Если отрезки AB и BC пересекают вертикальные прямые, то ломаная CDA их также пересекает, а горизонтальные прямые, соответственно, не пересекает. Тогда проекция ABCD на горизонтальную прямую имеет длину больше 1 (между A и C две вертикальных прямых), а на вертикальную – меньше 1, что невозможно.

  Если отрезки AB и BC пересекают (одну и ту же!) горизонтальную прямую, то ABCD лежит в полосе между двумя соседними вертикалями, а тогда AD и DC также пересекают горизонтальную прямую, что невозможно по тем же причинам.

  Остался единственный (с точностью до симметрии) случай – AB и CD пересекают одну и ту же вертикальную прямую v, а BC и AD – одну и ту же горизонтальную прямую h. Тогда A и B лежат под h, а C – над h, поэтому  BC > AB.  Аналогично B и C лежат правее v, а D – левее v, поэтому  BC < CD.

  Итак,  AB < BC < CD,  что невозможно.

Не может.