Олимпиадная задача по теории чисел: степени и делимость для 8–10 классов

Решение 1:   Пусть условие существует такая последовательность натуральных чисел c_n, что 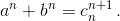   Ясно, что  c_n ≤ a + b,  так как иначе  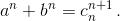  Значит, в последовательности c_n хотя бы одно число  c ≤ a + b  повторяется бесконечно много раз, то есть уравнение

aⁿ + bⁿ = cⁿ⁺¹  (с фиксированными a, b, c) имеет бесконечно много решений в натуральных n.

  Пусть для определенности  a ≥ b.  Перепишем уравнение  aⁿ + bⁿ = cⁿ⁺¹  в виде  (^a/_c)ⁿ + (^b/_c)ⁿ = c.

  Если  a > c,  то  ^a/_c = 1 + d,  где  d > 0.  Но тогда  (^a/_c)ⁿ + (^b/_c)ⁿ > (^a/_c)ⁿ = (1 + d)ⁿ > 1 + nd,  что больше c при  n > ^c/_d,  то есть число решений уравнения конечно.

  Если  a ≤ c,  то  (^a/_c)ⁿ ≤ 1  и  (^b/_c)ⁿ ≤ 1,  откуда  c = 2  или  c = 1.  Первый случай возможен только при равенстве  ^a/_c = ^b/_c = 1,  то есть при  a = b = 2.  Этот случай удовлетворяет условию задачи. Второй случай, очевидно, невозможен.

Решение 2:   Лемма. Если  (z, t) = 1,  то  (z + t, z² – zt + t²) = 1 или 3.

  Доказательство. Это сразу следует из равенства  z² – zt + t² = (z + t)² – 3zt.   Обозначим  d = (a, b),  a = dx,  b = dy.  Докажем вначале, что  x = y = 1.  Предположив противное, имеем  x^k + y^k > x^m + y^m  при  k > m; в частности, для чисел  D_n = x^2·3n + y^2·3n  имеем  D_n+1 > D_n  при любом натуральном n. Пусть p_n – некоторый простой делитель натурального числа  ^D_n+1/_Dn > 1.

  Заметим, что  p_n ≠ 3  (согласно задаче 208744, если сумма квадратов двух чисел кратна 3, то оба числа кратны 3, а x и y взаимно просты). По лемме D_n не делится на p_n, и в разложение на простые множители любого числа D_l, где  l ≥ n + 1,  число p_n входит в одной и той же степени (для доказательства второго утверждения нужно заметить, что число  ^D_n+k+1/_Dn+k  не делится на p_n, так как D_n+k делится на p_n). Поэтому  p_n ≠ p_k  при  n ≠ k.  Очевидно, в последовательности попарно различных чисел p₁, p₂, ... можно выбрать такое  p = p_n0,  что  (p, d) = 1.  В разложение любого числа d²3^lD_l,  где l ≥ n₀ + 1,  простой множитель p входит в одной и той же степени. С другой стороны, из условия следует, что эта степень делится на  2·3^l + 1  при любом натуральном  l ≥ n₀ + 1.  Противоречие.

  Итак,  a = b = d.  Очевидно,  d ≠ 1;  пусть простое число p входит в разложение d на простые множители в степени α. Рассмотрим два случая.

  1)  p ≠ 2.  Из условия следует, что nα делится на  n + 1  при любом натуральном n; значит, α делится на n + 1,  что невозможно.

  2)  p = 2.  Тогда  1 + nα  делится на n + 1  при любом натуральном n, значит,  1 – α  делится на  n + 1.  Отсюда  α = 1.

  Следовательно, d = 2.

(2, 2).