Олимпиадная задача по теории чисел: делимость членов арифметической прогрессии, 9-10 класс
Задача
Арифметическая прогрессия a1, a2, ..., состоящая из натуральных чисел, такова, что при любом n произведение anan+31 делится на 2005.
Можно ли утверждать, что все члены прогрессии делятся на 2005?
Решение
Пусть d – разность прогрессии. Если для всех n число an+31 кратно 5, то d кратно 5. Если же при некотором n число an+31 не кратно 5, то an кратно 5 и an+62 кратно 5, значит, an+62 – an = 62d кратно 5. Но тогда d кратно 5, поскольку 5 и 62 взаимно просты. Итак, в любом случае d кратно 5. Отсюда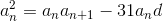 
кратно 5, и, поскольку 5 – простое число, an кратно 5.
Аналогично, пользуясь простотой числа 401, получаем, что an кратно 401.
Поскольку 5 и 401 взаимно просты, an делится на 5·401 = 2005 при любом n.
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь