Олимпиадная задача по геометрии: площадь четырехугольника и симметрия, 9–11 класс
Задача
Каждую вершину выпуклого четырехугольника площади S отразили симметрично относительно диагонали, не
содержащей эту вершину. Обозначим площадь получившегося четырехугольника через S' . Докажите, что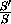 
<3.
Решение
При указанном отражении сохраняются длины диагоналей четырехугольника.
Пусть острый угол между диагоналями был равен α, тогда после отражения один из углов между диагоналями становится равным либо 3α, либо
3α-π , а поэтому отношение площадей равно
|
| .
Используя формулу для синуса тройного угла, получим,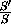 
=|3-4 sin2α|<3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет