Олимпиадная задача по рациональным функциям для 8–11 классов от Женодарова Р. Г.
Задача
Известно, что существует число S , такое, что если a+b+c+d=S и 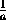 +
+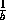 +
+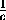 +
+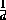 =S ( a , b , c , d отличны от нуля и единицы), то
=S ( a , b , c , d отличны от нуля и единицы), то 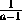 +
+ 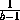 +
+ 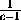 +
+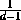 = S . Найти S .
= S . Найти S .
Решение
Если числа a , b , c , d удовлетворяют условиям утверждения в задаче, то числа 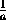 ,
, 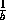 ,
, 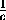 ,
, 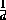 удовлетворяют этим условиям, а значит, для тех и других верно
заключение этого утверждения, т.е.
удовлетворяют этим условиям, а значит, для тех и других верно
заключение этого утверждения, т.е. 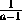 +
+ 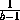 +
+ 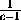 +
+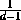 = S и
= S и 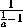 +
+ 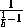 +
+ 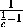 +
+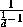 =S .
Сложив эти равенства, получим -4=2S , ибо
=S .
Сложив эти равенства, получим -4=2S , ибо 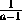 +
+ 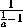 =-1,
откуда S=-2.
=-1,
откуда S=-2.
Нетрудно убедиться, что верно следующее утверждение:
если a+b+c+d=-2и 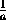 +
+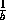 +
+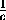 +
+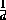 =-2( a , b , c , d отличны от нуля и единицы),
то
=-2( a , b , c , d отличны от нуля и единицы),
то 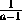 +
+ 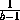 +
+ 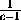 +
+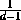 = -2.
Но этого в задаче не требуется.
= -2.
Но этого в задаче не требуется.
Ответ
-2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет