Назад

Олимпиадная задача по планиметрии для 7-9 класса от Агаханова Н.Х.

Задача 210167 • Сложность: 3 • 7-9 класс
Задача

В остроугольном треугольнике расстояние от середины каждой стороны до противоположной вершины равно сумме расстояний от неё до сторон треугольника. Докажите, что этот треугольник – равносторонний.

Авторы:
Агаханов Н. Х.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2003-2004 Региональный этап
Количество версий:
4
Решение

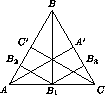
  Пусть A1, B1, C1 – середины сторон BC, CA, AB треугольника ABC, B2 и B3 – проекции точки B1 на стороны BA и BC(см. рис.), AA', BB' и CC' – высоты треугольника ABC.

  ТогдаB1B2– средняя линия треугольникаACC', то есть  B1B2= ½CC'.  Аналогично,  B1B3= ½AA'  и, значит,  BB1= ½ (AA' + CC').   Аналогично  CC1= ½ (AA' + BB'), AA1= ½ (BB' + CC'),  откуда  AA1+BB1+CC1=AA' + BB' + CC'.  НоAA1– наклонная,AA'– перпендикуляр, то есть AA1≥AA', причём равенство выполняется только еслиA1совпадает сA'.   Если хотя бы одно из трёх подобных неравенств строгое, то  AA1+BB1+CC1>AA' + BB' + CC',  что неверно.   Значит,A1совпадает сA', то есть медиана является высотой, поэтому  BA = CA.  Аналогично  AB = BC.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет