Олимпиадная задача Агаханова: доказательство неравенства с корнями и модулями, 9–11 класс
Задача
Положительные числа x, y, z таковы, что модуль разности любых двух из них меньше 2.
Докажите, что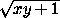  
+ 
+ 
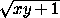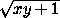> x + y + z.
Решение
По условию |x – y| < 2 ⇒ x² – 2xy + y² < 4 ⇒ x² + 2xy + y² < 4(1 + xy) ⇒ x + y < 2 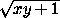. Аналогично
y + z < 2 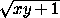, z + x < 2 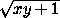⇒ 2x + 2y + 2z 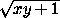< 2 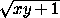+ 2 + 2 .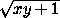
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет