Олимпиадная задача по планиметрии и производной для 9-11 классов от Емельянова Л. А.
Задача
Окружности σ 1 и σ 2 пересекаются в точках A и B . В точке A к σ 1 и σ 2 проведены соответственно касательные l1 и l2 . Точки T1 и T2 выбраны соответственно на окружностях σ 1 и σ 2 так, что угловые меры дуг T1A и AT2 равны (величина дуги окружности считается по часовой стрелке). Касательная t1 в точке T1 к окружности σ 1 пересекает l2 в точке M1 . Аналогично, касательная t2 в точке T2 к окружности σ 2 пересекает l1 в точке M2 . Докажите, что середины отрезков M1M2 находятся на одной прямой, не зависящей от положения точек T1 , T2 .
Решение
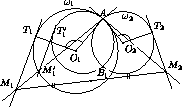
Пусть B1 – вторая (отличная от A ) точка пересечения σ 1' и σ 2 . Окружности σ 1' и σ 2 симметричны относительно прямой AB1 , причем при этой симметрии T1' переходит в T2 , t1' переходит в t2 , и M1' переходит в M2 . Таким образом, AM2=AM1'=kAM1 ( k не зависит от положения точек T1 и T2 ).
Тогда все треугольники AM1M2 гомотетичны с центром A (так как точки M1 и M2 лежат на прямых l1 и l2 , проходящих через A , по разные стороны от прямой AB1 , и отношение AM2:AM1 постоянно). Отсюда следует, что середины отрезков M1M2 лежат на фиксированной прямой, проходящей через точку A .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь