Олимпиадная задача: минимальный набор для покрытия пятизначных чисел с неубывающими цифрами

Набор с указанными свойствами не может состоять из одного числа. В самом деле: для каждого N=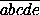 имеется различающееся с N во всех разрядах число G= 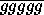, где g – цифра, отличная от нуля и от a , b , c , d , e . Покажем, что числа N₁= 13579и N₂= 12468образуют набор, удовлетворяющий условиям задачи.

Пусть A= – произвольное число, для цифр которого выполнены неравенства1 a₁ a₂ a₃ a₄ a₅ .

Тогда, если A не совпадает в разряде единиц ни с N₁ , ни с N₂ , то a₅ 7и, следовательно, a₄ 7; если при этом нет совпадений и в разряде десятков, то a₄ 5и a₃ 5.

Если, кроме того, нет совпадений и в разряде сотен, то a₃ 3, откуда a₂ 3; предположив еще, что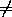 a₂ 2и a₂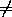 3, придем к равенству a₁ =1, означающему совпадение A с N₁ (и с N₂ ) в самом старшем разряде.

2.00