Олимпиадная задача: разрезание треугольника и сборка прямоугольника для 7–9 классов
Задача
Докажите, что произвольный треугольник можно разрезать на три многоугольника, один из которых должен быть тупоугольным треугольником, так, чтобы потом сложить из них прямоугольник. (Переворачивать части можно).
Решение
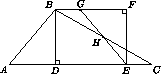
В неравнобедренном треугольнике ABC проведем высоту из вершины наибольшего угла
( BD на рис. 1). Пусть BC>BA , тогда DC>DA .
Прямоугольником, равновеликим треугольнику ABC будет прямоугольник BDEF ,
где DE=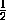 AC , а точка E лежит на DC , так как DC>DA .
Построим Δ GFE , равный Δ ADB ( G
AC , а точка E лежит на DC , так как DC>DA .
Построим Δ GFE , равный Δ ADB ( G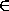 BF ).
Тогда BG=BF-GF=DE-AD=(AD+EC)-AD=EC , и из параллельности прямых BG и CE
BF ).
Тогда BG=BF-GF=DE-AD=(AD+EC)-AD=EC , и из параллельности прямых BG и CE 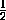 HBG=
HBG=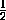 HCE ,
HCE , 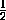 BGH=
BGH=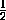 HEC .
Следовательно, Δ BGH=Δ CEH .
Получили три многоугольника: ABD , BDEH , CEH (тупоугольный треугольник).
Перекладывая Δ ABD на место Δ GEF и Δ CEH на место Δ BGH , получим прямоугольник.
HEC .
Следовательно, Δ BGH=Δ CEH .
Получили три многоугольника: ABD , BDEH , CEH (тупоугольный треугольник).
Перекладывая Δ ABD на место Δ GEF и Δ CEH на место Δ BGH , получим прямоугольник.
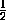
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь