Олимпиадная задача по планиметрии: окружности в треугольнике, Емельянов Л. А.
Задача
Пусть A0 – середина стороны BC треугольника ABC, а A' – точка касания с этой стороной вписанной окружности. Построим окружность Ω с центром в A0 и проходящую через A'. На других сторонах построим аналогичные окружности. Докажите, что если Ω касается описанной окружности на дуге BC, не содержащей A, то еще одна из построенных окружностей касается описанной окружности.
Решение
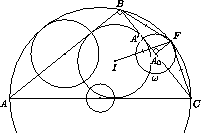
Первый способ. Обозначим через F точку касания Ω с описанной окружностью (см. рис.).
Так как A0F ⊥ BC, F – середина дуги BC. Если I – центр вписанной окружности треугольника ABC, то по лемме о трезубце (см. задачу 153119)
FB = FI = FC.
Так как IA' ⊥ BC, а A0A' = A0F, ∠IA'F = 90° + 45° = 135°. Следовательно, ∠BA'F = 135°. Треугольники BA'F и IA'F равны по двум сторонам и тупому углу ⇒ BA' = A'I = r ⇒ IBA' = 45° ⇒ ∠B = 2∠IBA' = 90°. Проводя те же рассуждения в обратном порядке, убеждаемся, что окружность, построенная для другого катета, также касается описанной.
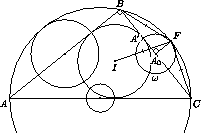
Так как F – середина дуги BC, то ∠FBA0 = α/2, FA0 = BA0 tg α/2 = a/2 tg α/2. Нетрудно видеть, что A0A' = |BA0 – BA'| = ½ |b – c|.
Пусть вписанная окружность касается стороны AC в точке B'. Тогда tg α/2 = IB'/AB' = r/p–a = s/p(p–a). В силу формулы Герона равенство FA0 = A0A' принимает вид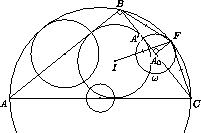 
a4 – a²(b – c)² = (b – c)²(b + c)² –a²(b – c)², a4 = (b² – c²)², a² = |b² – c²| ⇔ a² + c² = b² или a² + b² = c² ⇔ один из углов B, C – прямой.
Аналогичные выкладки показывают, что окружность, соответствующая второму катету, касается описанной.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь