Олимпиадная задача Агаханов Н.Х. по тригонометрии: равенство наборов sin и cos, 9–11 класс
Задача
Найдите все углы α , для которых набор чисел sinα , sin2α , sin3α совпадает с набором cosα , cos2α , cos3α .
Решение
α= +
+ .
Первое решение. Из совпадения наборов следует, что
.
Первое решение. Из совпадения наборов следует, что
- 1+2 cos x=0
 cos x=-
cos x=-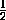
 x=
x=
 +2π n
+2π n
 sin3x=0, но 0 не принадлежит { cos x, cos2x, cos3x} .
sin3x=0, но 0 не принадлежит { cos x, cos2x, cos3x} .
- sin2x= cos2x
 tg2x=1, x=
tg2x=1, x= +
+ .
Наборы совпадают, так как
3x+x=
.
Наборы совпадают, так как
3x+x=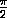 +2π n
+2π n cos3x= sin x , sin 3x= cos x .
cos3x= sin x , sin 3x= cos x .
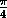 +π k , откуда α=
+π k , откуда α= +
+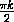 .
Непосредственной проверкой убеждаемся, что все углы указанного вида подходят.
.
Непосредственной проверкой убеждаемся, что все углы указанного вида подходят.
Осталось рассмотреть случай, когда сумма трех единичных векторов равна
нулю. Нетрудно видеть, что это возможно лишь если углы между ними равны  , откуда α=
, откуда α= +π k или α=
+π k или α=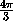 +π k . Легко видеть, что тогда sin3α=0, cosα
+π k . Легко видеть, что тогда sin3α=0, cosα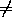 0, cos2α
0, cos2α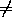 0и cos3α
0и cos3α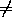 0.
0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет