Назад

Олимпиадная задача по планиметрии и стереометрии для 10–11 классов: симметрия прямых в тетраэдре

Задача 210124 • Сложность: 3 • 10-11 класс
Задача

Дан тетраэдрABCD. Вписанная в него сфера σ касается граниABCв точкеT. Сфера σ' касается граниABCв точкеT'и продолжений гранейABD, BCD, CAD. Докажите, что прямыеATиAT'симметричны относительно биссектрисы углаBAC.

Авторы:
Заславский А. А.
Разделы:
Планиметрия Стереометрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2002-2003 Региональный этап
Количество версий:
4
Решение

  Обозначим через M, M' точки касания сфер σ, σ' с плоскостью ABD, а через N, N' – точки касания сфер σ, σ' с плоскостью ACD соответственно (см. рис.). Пусть D' – некоторая точка на продолжении отрезка AD за точку A.

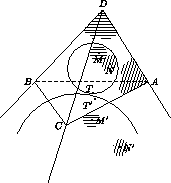
  Из равенства отрезков касательных, проведённых из одной точки к сфере, получаем:  DM = DN,  D'M' = D'N',  BM = BT,  CN = CT,  BM' = BT',  CN' = CT',

AM = AN = AT,  AM' = AN' = AT'.   Отсюда следуют равенства треугольников (по трём сторонам):DMAиDNA, D'M'AиD'N'A, ABMиABT, ABM'иABT', ACNиACT, ACN'иACT'.   Из выписанных равенств ∠BAT+ ∠BAT'= ∠BAM+ ∠BAM'= ∠MAM'= 180° – ∠DAM– ∠D'AM'= 180° – ∠DAN– ∠D'AN'= ∠NAN'= ∠CAN+ ∠CAN'= ∠CAT+ ∠CAT'.   Итак,  ∠BAT– ∠CAT= ∠CAT'– ∠BAT',  откуда ∠BAT= ∠CAT',  что и требовалось.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет