Олимпиадная задача: Два пирата и делёж добычи с алмазом — теория алгоритмов 7-9 класс
Задача
Два пирата делят добычу, состоящую из двух мешков монет и алмаза, действуя по следующим правилам. Вначале первый пират забирает себе из любого мешка несколько монет и перекладывает из этого мешка в другой такое же количество монет. Затем также поступает второй пират (выбирая мешок, из которого он берет монеты, по своему усмотрению) и т.д. до тех пор, пока можно брать монеты по этим правилам. Пирату, взявшему монеты последним, достается алмаз. Кому достанется алмаз, если каждый из пиратов старается получить его? Дайте ответ в зависимости от первоначального количества монет в мешках.
Решение
Рассмотрим случай, когда количество монет в мешках различается не более, чем на 1. Пусть второй пират на каждом шагу берет столько же монет, что и первый, но из другого мешка. Нетрудно убедиться, что в этом случае второй всегда может сделать ответный ход. Каждый раз после хода второго пирата разность числа монет в мешках будет той же, что в начале, значит, после некоторого его хода в одном мешке монет вообще не будет, а в другом будет не более одного, значит, первый пират не сможет сделать ход и проиграет.
В другом случае – если разность больше 1 – первый пират своим ходом забирает из большего мешка m монет,
если разность имеет вид3m или3m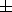
1,
чем приводит количество монет в мешках к первому случаю и дальше использует описанную
выше стратегию.
Ответ
Если количество монет в мешках различается не более, чем на 1, то алмаз достанется второму пирату, в противном случае – первому.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь