Олимпиадная задача: Модуль числа и тригонометрия, 10–11 класс, Знак Е.
Задача
Существует ли функция f(x), определенная при всех x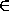
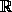и для всех x,y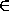 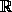удовлетворяющая неравенству
|f(x+y)+ sin x+ sin y|<2?
Решение
Пусть такая функция f(x)существует.
Положив в данном неравенстве x=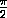
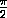, y= , получаем |f(π)+2|<2, т.е. f(π)<0. В то же время для x=
, y=-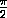 получаем |f(π)-2|<2, т.е. f(π)>0. Противоречие.
Ответ
Не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет