Олимпиадная задача по многочленам и примерам: пять корней, Агаханов, 9-11 классы
Задача
Докажите, что можно выбрать такие различные действительные числа a1, a2, ..., a10, что уравнение
(x – a1)(x – a2)...(x – a10) = (x + a1)(x + a2)...(x + a10) будет иметь ровно пять различных действительных корней.
Решение
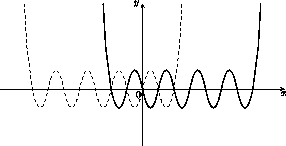
x = 0, ±1, ±2 (см. рис.). Сократив на общий множитель, (x – 2)(x – 1)x(x + 1)(x + 2) получаем: (x + 7)(x + 6)...(x + 3) = (x – 7)(x – 6)...(x – 3), то есть
(7 + 6 + 5 + 4 + 3)x4 + (7·6·5 + 7·6·4 + ... + 5·4·3)x² + 7·6·5·4·3 = 0. Это уравнение корней не имеет, так как левая часть, очевидно, положительна.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет