Олимпиадная задача по планиметрии для 8–9 классов: RX = RY в треугольнике
Задача
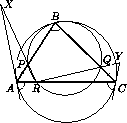
На сторонах AB, BC, CA треугольника ABC выбраны точки P, Q, R соответственно таким образом, что AP = CQ и четырёхугольник RPBQ– вписанный. Касательные к описанной окружности треугольника ABC в точках A и C пересекают прямые RP и RQ в точках X и Y соответственно. Докажите, что RX = RY.
Решение
Заметим, что поскольку ∠ARP < ∠ARP + ∠QRC = ∠B, то точка X лежит на луче RP (иначе ∠ARP = π – ∠ARX > ∠RAX = ∠B) (см. рис.). Значит,
∠ACB = ∠XAB и ∠APX = ∠RPB = ∠RQC, и треугольники APX и CQR равны по стороне и двум углам. Следовательно, PX = QR. Аналогично PR = QY, откуда и следует утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет