Задачи Подборки Авторы

Олимпиадная задача по теории чисел: убывающие делители и натуральные числа

Задача 209854 • Сложность: 3 • 8-10 класс

Задача

Пусть a₁, a₂, ..., a₁₀ – натуральные числа, a₁ < a₂ < ... < a₁₀. Пусть b_k – наибольший делитель a_k, меньший a_k. Оказалось, что b₁ > b₂ > ... > b₁₀.

Докажите, что a₁₀ > 500.

Решение

Заметим, что b_k = ^a_k/_{c_k} , где c_k – наименьший простой делитель a_k. Из неравенств a_i < a_i+1, b_i > b_i+1 следует, что c_i < c_i+1, то есть c₁ < c₂ < ... < c₁₀. Значит, c₉ ≥ 23, так как 23 – девятое по счёту простое число.

Так как b₉ > b₁₀, то b₉ > 1 и b₉ ≥ c₉. Отсюда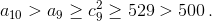

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться

Комментариев нет

Олимпиадная задача по теории чисел: убывающие делители и натуральные числа

Задача

Решение

Ответ

Подтверждение удаления