Олимпиадная задача по планиметрии: точки на окружности и равноудалённость центров
Задача
На дугах AB и BC окружности, описанной около треугольника ABC, выбраны соответственно точки K и L так, что прямые KL и AC параллельны.
Докажите, что центры вписанных окружностей треугольников ABK и CBL равноудалены от середины дуги ABC.
Решение
Если AB = BC, то утверждение очевидно.
Пусть для определенности AB < BC (см. рис.).
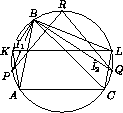
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет