Олимпиадная задача по планиметрии: Окружности в треугольнике с героем K для 8–11 класса
Задача
Окружность σ касается равных сторон AB и AC равнобедренного треугольника ABC и пересекает сторону BC в точках K и L . Отрезок AK пересекает σ второй раз в точке M . Точки P и Q симметричны точке K относительно точек B и C соответственно. Докажите, что описанная окружность треугольника PMQ касается окружности σ .
Решение
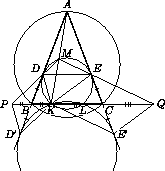
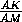 окружность σ переходит в окружность σ' . Окружность σ' проходит через точку K , а следовательно, и через L (из
симметрии относительно биссектрисы угла BAC ), а также σ' касается лучей AB и AC в некоторых точках D' и E' .
окружность σ переходит в окружность σ' . Окружность σ' проходит через точку K , а следовательно, и через L (из
симметрии относительно биссектрисы угла BAC ), а также σ' касается лучей AB и AC в некоторых точках D' и E' .
Из гомотетии следует, что MD|| KD' . Далее, по теореме о произведении отрезков касательных BD2=BK· BL = BD'2 , откуда BD=BD' . По построению BK=BP , поэтому DKD'P – параллелограмм, и значит, PD|| KD' . Отсюда вытекает, что точки M , D , P лежат на одной прямой. Аналогично, M , E и Q лежат на одной прямой. Треугольники MDE и MPQ гомотетичны с центром M , следовательно, их описанные окружности также гомотетичны, т.е. касаются в точке M .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь