Олимпиадная задача по планиметрии: радиусы описанных окружностей в треугольниках

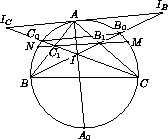
  Пусть биссектрисы AI, BI, CI пересекают описанную окружность в точках A₀, B₀ и C₀ соответственно. Точки B₀ и C₀ являются соответственно серединами дуг AC и AB.

  Проведём через A прямую, параллельную B₀C₀, пересекающую биссектрисы в точках I_B и I_C (см. рис.).

  Имеем  ∠AIB₀= ∠ABI+ ∠BAI= ∠ABB₀+ ∠BAA₀= ∠B₀BC+ ∠CAA₀= ∠B₀AI,  поэтому треугольникB₀AI– равнобедренный  (B₀A = BI).  Аналогично C₀A = CI,  поэтому треугольникиB₀AC₀иB₀IC₀равны.   ОтрезокB₀C₀является серединным перпендикуляром кAI, аAI– высота треугольникаII_BI_C. Отсюда следует, чтоB₀C₀– средняя линия треугольникаI_BII_C.   Получаем следующие равенства для радиусов описанных окружностей:R(I_BII_C) = 2R(B₀IC₀) = 2R(B₀AC₀) = 2R(ABC).   Теперь достаточно доказать, что точкиMиNлежат на описанной окружности треугольникаI_BII_C.   Заметим, что  ∠AI_BI= ∠C₀B₀I= ∠C₀B₀A= ∠C₀CA= ∠ICA,  значит, точки A, I, C, I_B лежат на одной окружности, откуда  B₁A·B₁C = B₁I·B₁I_B.  С другой стороны,  B₁A·B₁C = B₁M·B₁N,  так как точкиA, M, C, Nлежат на одной окружности.   Следовательно,  B₁M· B₁N = B₁I·B₁I_B,  и точкаI_Bлежит на описанной окружности треугольникаIMN. Аналогично на ней лежит точкаI_C.

Ответ задачи отсутствует