Олимпиадная задача по тригонометрии и производным: доказательство неравенства (10-11 класс)
Задача
Докажите, что sin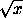 <
<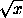 при0<x<
при0<x<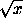 .
.
Решение
При x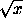 1имеем1
1имеем1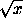
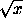
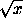 x<
x<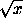 .
Отсюда sin
.
Отсюда sin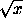
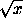 sin x . Далее, поскольку0< sin x<1,
имеем sin x<
sin x . Далее, поскольку0< sin x<1,
имеем sin x<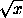 . Пусть0<x<1. Перепишем неравенство: sin2t< sin(t2)при0<t<1. Так как sin20= sin(02), то достаточно доказать( sin2t)'<( sin(t2))' , или2 sin t cos t<2t cos(t2).
Поскольку
. Пусть0<x<1. Перепишем неравенство: sin2t< sin(t2)при0<t<1. Так как sin20= sin(02), то достаточно доказать( sin2t)'<( sin(t2))' , или2 sin t cos t<2t cos(t2).
Поскольку 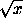 >t>t2>0, то cos t< cos (t2).
Перемножив это неравенство и sin t<t ,
получим sin t cos t<t cos(t2).
>t>t2>0, то cos t< cos (t2).
Перемножив это неравенство и sin t<t ,
получим sin t cos t<t cos(t2).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет