Олимпиадная задача по математике: Определение чисел на карточках за минимальные вопросы
Задача
На оборотных сторонах 2005 карточек написаны различные числа (на каждой по одному). За один вопрос разрешается указать на любые три карточки и узнать множество чисел, написанных на них. За какое наименьшее число вопросов можно узнать, какие числа записаны на каждой карточке?
Решение
Пусть было задано N вопросов. Ясно, что каждая карточка участвует хотя бы в одном вопросе, иначе число на ней мы не определим.
Пусть есть k карточек, участвующих ровно в одном вопросе. Тогда в одном вопросе не может встретиться двух таких карточек. Действительно, если бы две таких карточки участвовали в одном вопросе, то, поменяв местами числа на этих карточках, мы не изменим ответов на вопросы; поэтому невозможно установить, какое число на которой из них написано.
Следовательно, k
N . Остальные
карточки участвовали хотя бы в двух вопросах. Теперь, просуммировав для
каждой карточки количество вопросов, в которых она участвовала, получим
утроенное количество вопросов.
Поэтому3N
k+2(2005-k)=4010-k4010-N , откуда2N 2005, N 1003.
Приведем способ узнать числа за 1003 вопроса. Отложим одну карточку, а остальные разобьем на 334 группы по 6 карточек. В каждой группе занумеруем карточки числами от 1 до 6 и зададим три вопроса:(1,2,3),(3,4,5)и(5,6,1).
Тогда числа на карточках 1, 3, 5 встречаются в двух ответах (для разных
карточек– в разных парах) и поэтому однозначно определяются, а числа на
карточках 2, 4, 6– оставшиеся числа в каждом из ответов.
Так за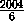 
x 3=1002вопроса мы узнаем числа на 2004 карточках.
Осталось спросить про отложенную карточку вместе с любыми двумя уже известными.
Ответ
За 1003 вопроса.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь