Задачи Подборки Авторы

Олимпиадная задача по функциям одной переменной для 9-11 классов от Агаханов Н. Х.

Задача 209819 • Сложность: 3 • 9-11 класс

Задача

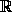
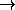
Существует ли ограниченная функция f : 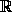такая, что f(1)>0и f(x)удовлетворяет при всех x,y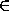 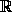неравенству

f²(x+y) f²(x)+2f(xy)+f²(y)?

Решение

Возьмем произвольно x₁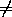0и положим y₁= 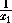. Тогда f²(x₁+y₁) f²(x₁)+2f(1)+f²(y₁) f²(x₁)+a , где a=2f(1)>0. Будем далее выбирать x_n=x_n-1+y_n-1, y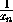_n= , n2. Тогда f²(x_n+y_n) f²(x_n)+a=f²(x_n-1+y_n-1)+a f²(x_n-1)+2a.. f²(x₁)+na . Ясно, что последовательность f(x₁), f(x₂), f(x_n), неограничена.