Олимпиадная задача по многочленам для 9–11 классов от Голованова А. С.
Задача
Многочлены P, Q и R с действительными коэффициентами, среди которых есть многочлен второй степени и многочлен третьей степени, удовлетворяют равенству P² + Q² = R². Докажите, что все корни одного из многочленов третьей степени – действительные.
Решение
Из условия следует, что R и один из многочленов P и Q – третьей степени. Пусть, например, R и Q – третьей степени, а P – второй. Поменяв, если нужно, знаки многочленов на противоположные, можно считать, что коэффициенты при x³ у R и Q положительны. Тогда из равенства
P² = R² – Q² = (R + Q)(R – Q), где R + Q – третьей степени, следует, что R – Q – первой степени, то есть R – Q = c(x – x1), c > 0 (коэффициент при x4 у P² положителен). Тогда P, а значит, и R + Q делятся на x – x1. Так как и R – Q делится на x – x1, то R и Q делятся на x – x1, то есть R = (x – x1)R1,
Q = (x – x1)Q1, где R1 и Q1 – квадратичные функции с положительными коэффициентами при x². При этом R1 – Q1 = c, R1 = Q1 + c.
Пусть P = a(x – x1)(x – x2). Тогда a²(x – x2)² = (2Q1 + c)c, то есть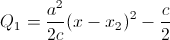 
– трёхчлен, имеющий два действительных корня. Значит, Q имеет три действительных корня.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь