Олимпиадная задача по комбинаторной геометрии и алгебраическим методам для 9–11 классов
Задача
В квадрате n×n клеток бесконечной шахматной доски расположены n2 фишек, по одной фишке в каждой клетке. Ходом называется перепрыгивание
любой фишкой через соседнюю по стороне фишку,
непосредственно за которой следует свободная клетка.
При этом фишка, через которую перепрыгнули, с доски снимается. Докажите, что
позиция, в которой дальнейшие ходы невозможны, возникнет не ранее, чем через[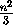 ]ходов.
]ходов.
Решение
Будем различать два типа ходов – внутренние и внешние, в зависимости от того, куда ставится фишка, делающая ход: внутрь исходного квадрата n×n клеток, или вне его.
Пусть получена позиция, где дальнейшие ходы невозможны, причем сделано k внутренних ходов и l внешних.
Ясно, что никакие две фишки не находятся в соседних клетках; поэтому в исходном
квадрате n×n не менее чем[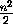 ]клеток пусты. Действительно, нетрудно понять, что квадрат
разрезается на доминошки (в случае четной стороны) или доминошки и
одну угловую клетку (в случае нечетной), а в каждой доминошке есть хотя бы одна пустая клетка.
Так как каждый внутренний ход увеличивал количество пустых клеток
не более, чем на 1, а каждый внешний – не более, чем на 2, то имеем
неравенство
]клеток пусты. Действительно, нетрудно понять, что квадрат
разрезается на доминошки (в случае четной стороны) или доминошки и
одну угловую клетку (в случае нечетной), а в каждой доминошке есть хотя бы одна пустая клетка.
Так как каждый внутренний ход увеличивал количество пустых клеток
не более, чем на 1, а каждый внешний – не более, чем на 2, то имеем
неравенство
k+2l [
[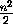 ].
(1)
].
(1)
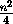 четырехклеточных квадратиков и заметим, что на каждый
квадратик пришлось не менее двух ходов, в которых участвовали
(делали ход или снимались с доски) фишки, стоявшие в клетках этого
квадратика. Поскольку в каждом внутреннем ходе участвовали фишки не более,
чем двух квадратиков, а в каждом внешнем – не более, чем одного, то
четырехклеточных квадратиков и заметим, что на каждый
квадратик пришлось не менее двух ходов, в которых участвовали
(делали ход или снимались с доски) фишки, стоявшие в клетках этого
квадратика. Поскольку в каждом внутреннем ходе участвовали фишки не более,
чем двух квадратиков, а в каждом внешнем – не более, чем одного, то
 2
2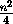 .
(2)
.
(2)
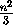
 [
[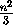 ], т.е. утверждение
задачи в этом случае верно.
], т.е. утверждение
задачи в этом случае верно.
Легко видеть, что оно верно также при n=1и при n=3.
В случае n=2m+1, где m>1, в кресте, образованном третьей сверху горизонталью и третьей слева вертикалью, выделим2m доминошек, а остальную часть исходного квадрата разобьем на m2 четырехклеточных квадратиков. В каждом внутреннем ходе участвовать могли фишки, принадлежащие не более чем двум из m2+2m рассматриваемых фигур, а в каждом внешнем – не более чем одной. Имеем неравенство
 2m2+2m,
(3)
2m2+2m,
(3)Из(1)и(3)следует, что3(k+l) 4m2+4m=n2-1. Если здесь n2кратно 3, то, очевидно,3(k+l)
4m2+4m=n2-1. Если здесь n2кратно 3, то, очевидно,3(k+l) n2 и k+l
n2 и k+l
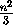 =[
=[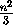 ], в противном случае n2сравнимо с 1 по модулю 3 и k+l
], в противном случае n2сравнимо с 1 по модулю 3 и k+l
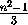 =[
=[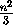 ].
Тем самым утверждение задачи полностью доказано.
].
Тем самым утверждение задачи полностью доказано.
Можно доказать, что для любого ε>0при достаточно больших n количество
ходов будет больше, чем n2(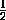 -ε). Один
из методов доказательства заключается в следующем.
-ε). Один
из методов доказательства заключается в следующем.
Предположим противное.
Рассмотрим
каемку нашего квадрата ширины 2, каемку квадрата,
получающегося выкидыванием первой, и т.д., всего k=[nε/8]каемок. Заметим, что внутри последней каемки
содержится хотя бы n2(1-ε/2)2>n2(1-ε/4)клеток. Тогда за максимум n2(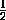 -ε)ходов из
нашего квадрата ушло хотя бы[
-ε)ходов из
нашего квадрата ушло хотя бы[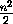 ]
]
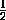 n2(1-ε)фишек;
значит, было хотя бы
n2(1-ε)фишек;
значит, было хотя бы 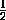 ε n2 ходов, на которых
количество фишек в нем уменьшалось на 2; эти ходы вели из первой
каемки вовне, и не затрагивали квадрата внутри первой каемки.
Тогда за не более чем n2(
ε n2 ходов, на которых
количество фишек в нем уменьшалось на 2; эти ходы вели из первой
каемки вовне, и не затрагивали квадрата внутри первой каемки.
Тогда за не более чем n2(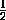 -
-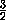 ε)ходов
из следующего по величине квадрата ушло хотя бы
ε)ходов
из следующего по величине квадрата ушло хотя бы 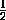 n2(1-ε)фишек;
значит, было хотя бы ε n2 ходов, на которых
количество фишек в нем уменьшалось на 2; эти ходы вели из второй
каемки вовне. Аналогично, из третьей каемки вовне вело хотя бы2ε n2 ходов, из k -й каемки –2k-2ε n2 ходов.
Однако при больших n 2k-2ε n2=2[nε/8]-2ε
n2>n2 , т.е. ходов гораздо больше, чем предполагалось.
Противоречие.
n2(1-ε)фишек;
значит, было хотя бы ε n2 ходов, на которых
количество фишек в нем уменьшалось на 2; эти ходы вели из второй
каемки вовне. Аналогично, из третьей каемки вовне вело хотя бы2ε n2 ходов, из k -й каемки –2k-2ε n2 ходов.
Однако при больших n 2k-2ε n2=2[nε/8]-2ε
n2>n2 , т.е. ходов гораздо больше, чем предполагалось.
Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь