Олимпиадная задача по теории чисел: ограниченные последовательности 9-11 класс
Задача
Найдите все бесконечные ограниченные последовательности натуральных чисел a1, a2, a3, ..., для всех членов которых, начиная с третьего, выполнено
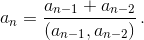
Решение
Пусть (ak, ak+1) = 1. Тогда (ak, ak+1) = (ak + ak + 1, ak+1) = (ak+2, ak+1), то есть для всех последующих членов последовательности НОД тоже будет равен 1. При этом, начиная с k-го члена, последовательность превращается в последовательность an = an–1 + an–2, которая неограниченно возрастает, что невозможно.
Значит, ak+2 ≤ ½ max{ak+1, ak} и max{ak+1, ak} не возрастает. Следовательно, когда-то он стабилизируется:
max{ak+1, ak} = max{ak+2, ak+1} = max{ak+3, ak+2} = ... = d.
Если при этом ak+1 ≠ ak, то ak+2 < d, ak+3 < d, что невозможно. Поэтому ak = ak+1 = ak+2 = ... = d, откуда d = 2. Следовательно,
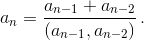 откуда ak–1 = 2, и последовательность состоит только из двоек.
откуда ak–1 = 2, и последовательность состоит только из двоек.
Ответ
a1 = a2 = ... = 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь