Олимпиадная задача по математике: свойства корней, функции и анализ — 9-11 класс
Задача
Докажите, что если(x+ )(y+
)(y+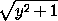 )=1, то x+y=0.
)=1, то x+y=0.
Решение
Умножая обе части данного неравенства на x- , получаем, что-y-
, получаем, что-y-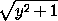 =x-
=x- . Аналогично, умножая обе части данного равенства на y-
. Аналогично, умножая обе части данного равенства на y-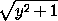 , приходим к равенству-x-
, приходим к равенству-x- =y-
=y-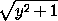 .
Складывая полученные равенства, приходим к равенству-(x+y)=x+y , откуда x+y=0.
.
Складывая полученные равенства, приходим к равенству-(x+y)=x+y , откуда x+y=0.
Заметим, что функция f(x)=x+ возрастает при x
возрастает при x 0; при x<0она также возрастает, так как f(x)=
0; при x<0она также возрастает, так как f(x)=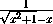 и знаменатель, очевидно, убывает.
Поэтому при фиксированном y у данного уравнения не больше одного
решения; с другой стороны, x=-y – очевидно, рещение уравнения.
и знаменатель, очевидно, убывает.
Поэтому при фиксированном y у данного уравнения не больше одного
решения; с другой стороны, x=-y – очевидно, рещение уравнения.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет