Олимпиадная задача по стереометрии для 10-11 класса: высоты и вписанная сфера тетраэдра

  Пусть плоскость CHD пересекается с прямой AB в точке E,  плоскость AHD с BC – в точке F, а плоскость BHD с CA – в точке G. Так как  CC₁ ⊥ AB  и

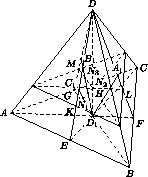
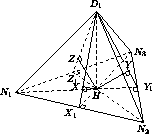
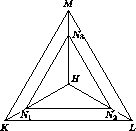
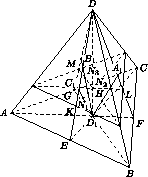
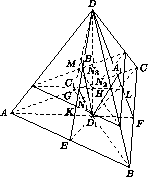
DD₁ ⊥ AB,  то  AB ⊥ CED,  то есть DE и CE – высоты треугольников ABD и ABC. Из аналогичных рассуждений для других рёбер следует, что точки A₁, B₁, C₁ и D₁ – ортоцентры граней тетраэдра ABCD. Из этого факта и из условия вытекает, что все грани данного тетраэдра являются остроугольными треугольниками. Как известно (см. задачу 152886), высоты остроугольного треугольника являются биссектрисами ортотреугольника, то есть ортоцентр остроугольного треугольника есть центр окружности, вписанной в ортотреугольник. Проведём через точку H плоскость α, параллельную плоскости ABC. Пусть α пересекается с прямыми DE, DF, DG, D₁C₁, D₁A₁, D₁B₁ соответственно в точках K, L, M, N₁, N₂, N₃ (рис. слева). Тогда сфера касается граней пирамиды D₁N₁N₂N₃, имеющих вершину D₁. Пусть X, Y, Z – точки касания (рис. справа).

  Поскольку  α ||ABC,  H– центр вписанной окружности треугольникаKLM. Прямоугольные треугольникиD₁HX, D₁HYиD₁HZравны по катету и гипотенузе. Из равенства угловXD₁H, YD₁HиZD₁Hследует равенство по катету и острому углу треугольниковD₁HX₁,D₁HY₁иD₁HZ₁, следовательно,  HX₁=HY₁=HZ₁,  то естьH– центр вписанной окружности треугольникаN₁N₂N₃.   Пусть  ∠MKL= 2θ,  ∠KLM= φ,  ∠LMK= ψ  (рис. слева). Тогда  ∠MHL= 90° + θ.  Если  ∠N₃N₁N₂= 2θ₁,  то аналогично  ∠N₃HN₂= 90° + θ₁= ∠MHL,  следовательно,  θ₁= θ,  значит,  N₁N₂||KL.  Аналогично  N₂N₃||LM  и  N₃N₁||KM.  Из подобия треугольников следует, что KN₁:N₁H = LN₂:N₂H = MN₃:N₃H  и (рис. в центре)  KN₁:N₁H = ED₁:D₁C,  LN₂:N₂H = FD₁:D₁A,  MN₃:N₃H = GD₁:D₁B.  Значит, ED₁:D₁C = FD₁:D₁A = GD₁:D₁B.   (1)  По теореме о пересекающихся хордах (рис. справа)  ED₁·D₁C = FD₁·D₁A = GD₁·D₁B.   (2)   Из (1) и (2) вытекает, что  ED₁=FD₁=GD₁,  а  D₁C = D₁A = D₁B,  то есть центры вписанной и описанной окружностей треугольникаABCсовпадают, поэтому этот треугольник – правильный. Аналогично правильными треугольниками являются и остальные грани тетраэдраABCD.

Ответ задачи отсутствует